NZD-99 : Home - Nen - Zen - Den - 99
Zen : A Decentralized Gold / Silver / Copper Monetary System.By Justus L. Ludovic.(Under Construction)

Video : English
Zen is a decentralized monetary system that use precious metal coins, their respective electronic cryptographic coins and layers of channel factories networks as money in a dozenal numerical base system.

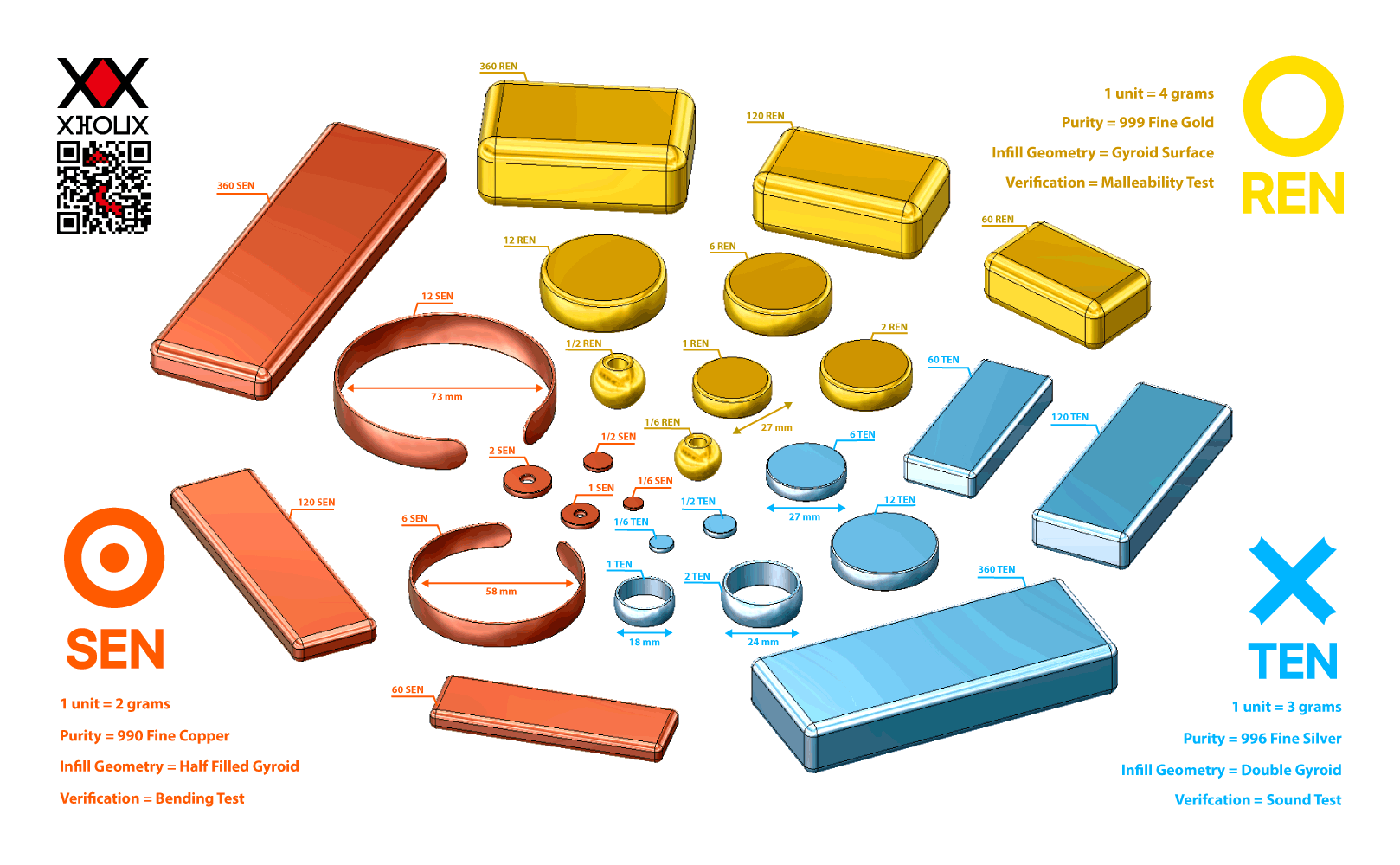
Gold Ren, Silver Ten and Copper Sen are 3 decentralized precious metal coins made from : Gold, Silver and Copper. The decentralized aspect of the coins is assured by the possibility to print the coins with any 3D Metal Desktop Printer with the right fineness powder. A minimal surface geometry is used so it can be easy to verify the coins by hand and hard to counterfeit in fineness.
Denomination :
For each coin. The different denominations are 9 types : 1/6 (An Hour), 1/2 (Three Hours), 1 (Full Day), 2 (Two Days), 6 (Full Week), 12 (Two Weeks), 60 (Two Months), 120 (Third of A Year) and 360 (A Year). These domination are made from Anti-Primes, numbers with the most divisors. It increase the combinaisons of weight verification between dominations. (on-coin verification)
The number of coins in circulation for each denomination follow the Metallic Mean Distribution. Where for a denomination D, its weight in the total in circulation is the inverse of (D + (D^2 + 4)^0.5)/2 the positive solution of X^2-DX-1 = 0 :
| D | W = 2/(D + (D^2 + 4)^0.5) | % in Circulation (W/Total(W)) | in Circulation for 1110 | Value in coin unit |
| 0,1666 (1/6) | 0,9201 | 0,3061 | 360 | 60 |
| 0,5 (1/2) | 0,7807 | 0,2597 | 280 | 140 |
| 1 | 0,6180 | 0,2056 | 220 | 220 |
| 2 | 0,4142 | 0,1377 | 150 | 300 |
| 6 | 0,1622 | 0,0539 | 60 | 360 |
| 12 | 0,0827 | 0,0275 | 30 | 360 |
| 60 | 0,0166 | 0,0055 | 6 | 360 |
| 120 | 0,0083 | 0,0027 | 3 | 360 |
| 360 | 0,0027 | 0,0009 | 1 | 360 |
| Total | 3,0059 | 1 | 1110 | 2520 |
In this denomination distribution, 91% of total denominations in circulation are : 1/6 (An Hour), 1/2 (Three Hours), 1 (Full Day) and 2 (Two Days). It store 28.5% of the total value in circulation.
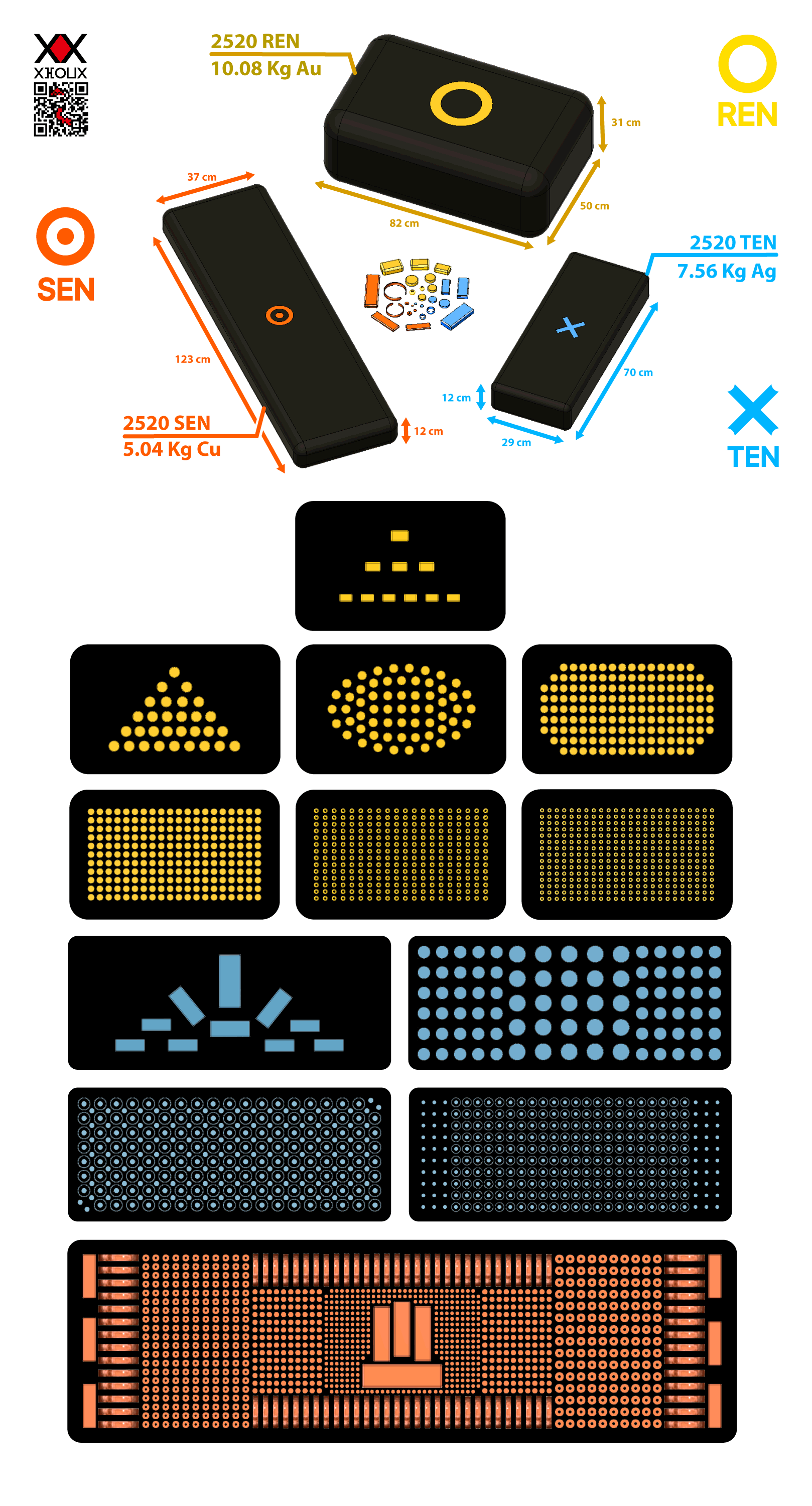
The total value of 1110 pieces in this distribution is exactly 2520. It's the next Anti-Prime after 360. A minted block with this characteristics It's called The God's Block. It's the 10th denomination of the coin that can be exchanged as money.
The coins are minted and enter the circulation by God's Blocks. In this way, the minting cost is shared by all the denominations of a block.
For recap, the 10 denomination of the Gold Ren, Silver Ten and Copper Sen coins are : 1/6 (An Hour), 1/2 (Three Hours), 1 (Full Day), 2 (Two Days), 6 (Full Week), 12 (Two Weeks), 60 (Two Months), 120 (Third of A Year), 360 (A Year) and 2520 (God's Block).
| D | Gold Ren | Silver Ten | Copper Sen |
| 1/6 (0,1666) | A Full Hour | A Twenty minutes | Ten Seconds |
| 1/2 (0,5) | Three Hours | 1 Hours | Half Minute |
| 1 | A Full Day | 2 Hours | A Full Minute |
| 2 | Two Days | 4 Hours | Two Minutes |
| 6 | A Full Week | Half a day | Six Minutes |
| 12 | Two Weeks | A Full Day | Dozen Minutes |
| 60 | Two Months | Five days | A Full Hour |
| 120 | Third of A Year | Ten days | Two Hours |
| 360 | A Full Year | A Full Month | A Full Day |
| 2520 | A Gold God's Block | A Silver God's Block | A Copper God's Block |
The names are a labor approximation value in that period of time. A full day labor cost around 1 Ren or 12 Ten or 360 Sen
Weight :
The weight of the Gold Ren is superior than the Silver Ten. And the weight of the Silver Ten is superior of the Copper Sen. This configuration help identify a denomination type by just feeling the weight.
The exact weight (x,y,z) of each coin is calculated by solving a 3 variables arithmetic equation.
For a (x,y,z) weight, the relative weight table for a denomination in n amount of each coins is as fellow :
| Gold Ren (n*x amount) | Silver Ten (n*y amount) | Copper Sen (n*z amount) | Total | |
| Gold Ren (x amount) | n | n*y/x | n*z/x | n*(1+(y+z)/x) |
| Silver Ten (y amount) | n*x/y | n | n*z/y | n*(1+(x+z)/y) |
| Copper Sen (z amount) | n*x/z | n*y/z | n*n | n*(1+(x+y)/z) |
| Total | n*(3+(y+z)/x+(x+z)/y+(x+y)/z) | |||
| Arithmetical Average | n*(3+(y+z)/x+(x+z)/y+(x+y)/z)/9 |
The arithmetical average is : n*(3+(y+z)/x+(x+z)/y+(x+y)/z)/9 = n*(3xyz+zyy+yzz+zxx+xzz+yxx+xyy)/9xyz
For a more optimal and easy weight comparaison. We chose the denomination of the dozenal base n = 12 and the constraint of the arithmetical average need to be an integer for x>y>z.
To solve the equation, we use python to find the smallest solution :
z = 1
y = z + 1
x = y + 1
n = 12
A = n*(3*x*y*z+z*y*y+y*z*z+z*x*x+x*z*z+y*x*x+x*y*y)
B = 9*x*y*z
while (A%B != 0) :
z = z + 1
if (z == y) :
z = 1
y = y + 1
if (x == y):
z = 1
y = z + 1
x = x + 1
A = n*(3*x*y*z+z*y*y+y*z*z+z*x*x+x*z*z+y*x*x+x*y*y)
B = 9*x*y*z
print "{} : {} : {} : {}\n".format(A/B,z,y,x)
The smallest solution is x=4, y=3 and z=2 with an arithmetical average of 13.
And with the use of the standard grams. It give to the Gold Ren a weight of 4.00 grams, Silver Ten a weight of 3.00 grams and Copper Sen a weight of 2.00 grams. This is approximately the recent Monetary System of Gold Solidus, Silver Drachmal and Copper Follis mined in the period of Rome and Greece.
For a dozen coins (12), the relative weight is as fellow :
| 12 Gold Ren (48 grams) | 12 Silver Ten (36 grams) | 12 Copper Sen (24 grams) | Total | |
| Gold Ren (4 grams) | 12 | 9 | 6 | 27 |
| Silver Ten (3 grams) | 16 | 12 | 8 | 36 |
| Copper Sen (2 grams) | 24 | 18 | 12 | 54 |
| Total | 117 | |||
| Arithmetical Average | 13 |
In average, a 12 coins denomination is equivalent in weight to 13 coins in another type. This make easy to verify weight of a coin with coins in different type. (cross-coin verification).
Shape :
Each denomination in a coin is one of the 3 shapes : a Disk shape, a Napkin ring shape or a Bar shape. Each shape is designed with one of the metallic mean of Gold (1.618…), Silver (2.414…) or Copper (3.303…).
The design are as fellow :
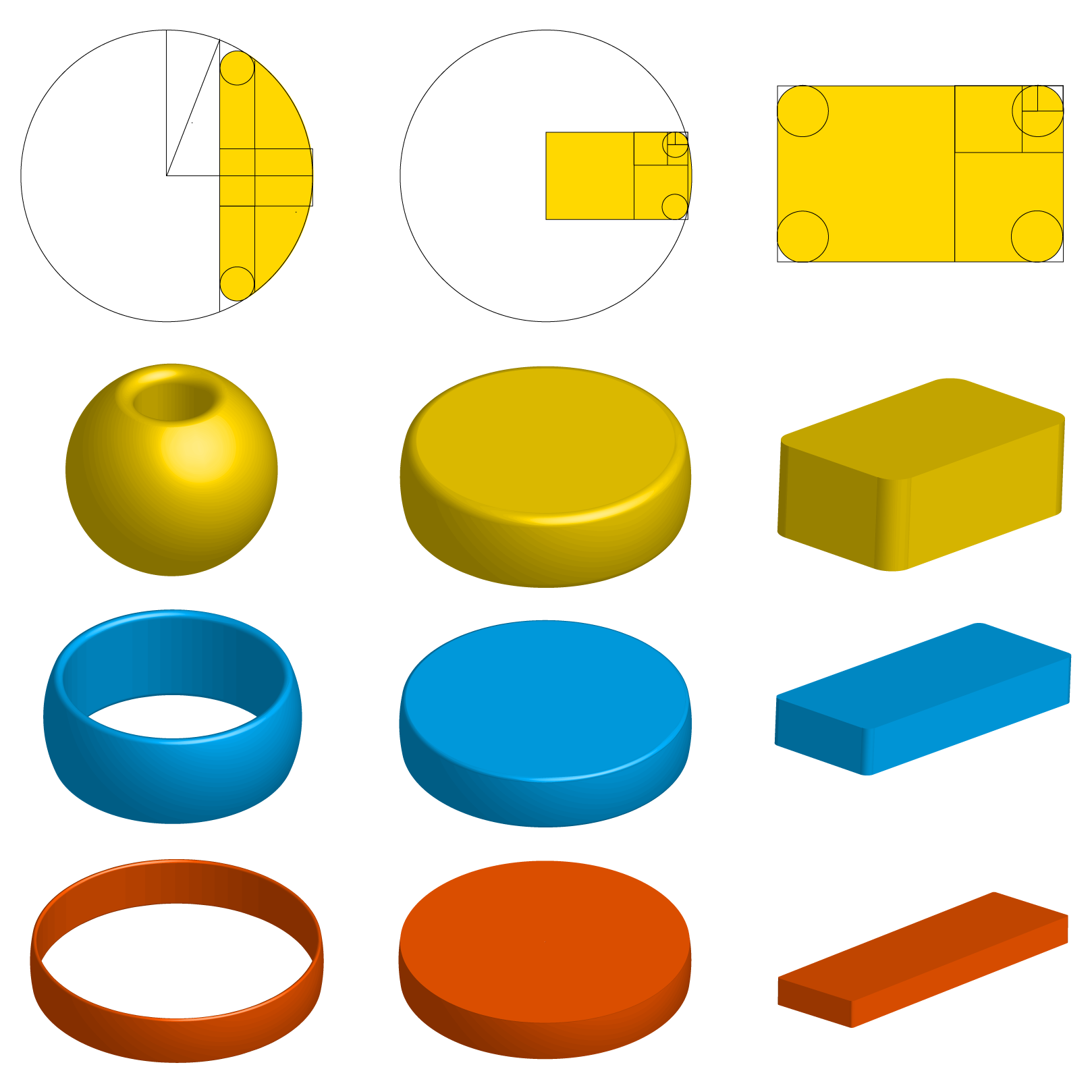
For the Napking Ring, the angle is 2*Pi/1.6180339^2
The distribution of the shape in coins and their denomination are as fellow :
| Denomination | Gold Ren | Silver Ten | Copper Sen |
| 1/6 (0,1666) | Napking Ring | Disk | Disk |
| 1/2 (0,5) | Napking Ring | Disk | Disk |
| 1 | Disk | Napking Ring | Disk |
| 2 | Disk | Napking Ring | Disk |
| 6 | Disk | Disk | Napking Ring |
| 12 | Disk | Disk | Napking Ring |
| 60 | Bar | Bar | Bar |
| 120 | Bar | Bar | Bar |
| 360 | Bar | Bar | Bar |
The Napking ring shape make the coin wearable. Gold Ren's Napking Ring is a Ornament Ball that can be weared on the women's ear or assembled as a colier in her neck. Silver Ten's Napking Ring is a finger Ring that can be weared in the fingers. Copper Sen's Napking Ring is a bracelet.
Amount :
The amount occupied by the metal in the shape's volume of the coin is proportionate to the denominations and the metallic mean of the coin. The ratio is measured per 360.
| Denomination | per 360 Volume (Gold Ren) | per 360 Volume (Silver Ten) | per 360 Volume (Copper Sen) |
| 1/6 (0,1666) | 7 (1.94%) | 176 (48.88%) | 330 (91.66%) |
| 1/2 (0,5) | 13 (36.11%) | 219 (60.83%) | 330 (91.66%) |
| 1 | 16 (4.44%) | 182 (50.55%) | 330 (91.66%) |
| 2 | 20 (5.55%) | 150 (41.66%) | 330 (91.66%) |
| 6 | 38 (10.05%) | 187 (51.94%) | 330 (91.66%) |
| 12 | 47 (13.05%) | 155 (43.05%) | 330 (91.66%) |
| 60 | 144 (40.00%) | 321 (89.16%) | 330 (91.66%) |
| 120 | 187 (49.44%) | 264 (73.33%) | 330 (91.66%) |
| 360 | 330 (91.66%) | 330 (91.66%) | 330 (91.66%) |
For Gold Ren and Silver Ten the volume of a denomination is proportionate to the metallic mean of the greater denomination.
For example, Let's calculate the volume ratio between 120 and 360 Gold Ren :
Volume of 360 gold coin is : 360/91.66% = 392.72 Volume of 120 gold coin is : 120/50.00% = 242.71 The Volume Ratio between the two volume is : 392.72/242.71 = 1.618…
Overview :
You can see an 3D Overview of all the coins below (click to enlarge):
For the God's Blocks and their coin arrangement (click to enlarge):
Fineness (Introduction to Den) :
The Fineness of the precious metals for each coins is closely related to the Den's Economical Believe System.
In the Believe System of Den (Which will be later introduced in detail by Isaac N. Meruem), we believe for a stable economy, healthy productivity growth and for a robust protection to crisis. A fraction of the stored wealth in gold in the economy must be distributed among people geometrically. The distribution must be in a way that if some global natural disaster happen and the world got through 19 years of frozen economy and difficult living for all people. And the wealthy ones keep distributing each year the fraction of what they have in gold to the people with the most in need. The wealthy must have left in gold the golden ratio (61.80%) of what they had before 19 years.
To solve this equation, the fraction that must be distributed should be : 1-0.6180339^(1/19) = 2.5%.
The distribution must be decentralized and given directly to the one in need. The priority between the people in need is as fellow : Pregnant Mother over Mother in Breasfeeding over Orphan Girl over Orphan Boy over Widow over Old Women over Old Man over Young Women over Young Man.
The top priority for a person in need are The Pregnant Mother. which can be any pregnant Women/Girl/Female/Uterus indifferent in her ethnicity or believes or what she did or who she is. If she is at her first week of pregnancy or at her last moment of pregnancy at labor pain. If she is a Pregnant little girl at her first period of puberty or pregnant old women at her last period before menopause. If she is Pregnant from her husband, or from her lover, or from a serial rapist, or from incest. If she is a slut pregnant by the Devil or a virgin pregnant by the grace of God. In The Believe System of Den, All Pregnant Mothers are equals. and it gives her the top priority if she have any need.
Then come after it the Mother who are in Breatfeeding of a baby. Where the baby can be her own or any baby from someone else. They are both have equal priority. Then come orphan girls and orphan boys whose one or both of their parents are dead or unknown. Where girls have priority over boys. Then come the Widows whose her spouse have died. Then come the old Women, old Men, Young Women and then at last priority a Young Man.
Just in quotes : "The three most beautiful creatures you can ever imagine are : a Pregnant Mother, a Mother Breastfeeding a baby and an Innocent Girl"
With this decentralized wealth distribution each year, it will remove all centralized institutions like gouvernement, military, taxation, stocks (and all trust/debt-based non-physical assets), health insurance, orphanage, retirement etc. It will help increase the productivity in the economy in the short and long run without the need of an inflation-deflation currency policy. And with the distribution reward to pregnant mothers as top priority, it will remove the sexual freedom illusion of condoms, birth controls and homosexuality, and encourage natural decentralized non-incestious monogamic/polygynic marriage where a young women have the exclusive right to marry herself to any young man she like, but she can't divorce herself. And a young man have the exclusive right to divorce himself from any young women he dislike, but he can't marry himself. And this is a fair zero sum game without the need of any centralized religious institution.
The economy will grow exponentially because the population will grow exponentially. And the distribution of wealth will distribute the people all across the land and make the lands more fertile and productive for people and nature. And the more a population get distributed across a land. The more difficult for an centralized military force to conquer and take control of the land and its people, and that no matter what military technology they are using. In short it will be a Decentralized global society ruled by no one except God.
This decentralized wealth distribution will also remove all interest on loans. In this type of economy, loans can only be 0% or with a theoretical negative interest.
For example, a 1000 gold coins loan that a lender give to a borrower for a period of 3 year must have a negative interest of exactly 0.6180339^(3/19)-1 = -7.31%
In practice, a negative interest loan can be set in 2 transactions. The first one is the distribution's transaction of 73.1 coins that the lender must give to the borrower in need if the lender intent to store 1000 gold coin for 3 years. And the second is a no interest loan of 926.9 coin that the borrower need to pay back to the lender after 3 years. Which mean in practice, if a borrower is in need, the lender must either distribute some of their stored wealth or give a loan without interest or both.
Just in quotes : "Interest on a loan is not paying for a service nor a good that the lender have given to the economy. An interest, it's the act of rewarding the lender just because he is wealthy."
"It's the act of legal stealing of wealth directly from people with the most crucial need to the most wealthy. The most evil and unforgivable Sin a man can do."
"It's the cause of the recent world disorder. The world were the rule of a law let strong nations (wealthy) eat the weak (poor)."
"It's the real life incarnation of "Selling Bricks as Apples of Tamarix". A code name of the most disturbing and disgusting creature you can ever imagine."
"I believe, It's stealing directly from the most desperate for help Pregnant Mothers which is, for humanity, one hundred fold more destructive than "Fucking His Own Mother". Therefore saying to a Banker "Good Morning! Motherfucker!" is a compliment."
In resume, in the Economy of Den we believe only on 3 types of transactions : Transactions of normal commerce of goods and services. It include trading of any objects made from different materials. (Nen's transaction) Transactions of trading by equal weight and amount any objects or good made with the same materials without interest in weight nor amount. It include lending money without interest. (Zen's transaction) Transactions of distributing stored wealth in gold among people in need with a minimum of 2.5% each year geometrically. (Den's transaction)
Fineness :
The Fineness range of Gold Ren is related to the formula used to calculate the 2.5% wealth distribution fraction of Den's transaction.
The impurity of the Gold Ren is at maximum the Distribution Rate of a year. With a theoretical minimum impurity of the Distribution rate of a Day. And a perfect impurity of the golden ratio between the two. Which mean :
Minimum Fineness : 0.6180339^(1/19) = 0.975 (23.5 Karat) Theoretical Maximum Fineness : 0.6180339^(1/(19*365.25)) = 0.9999 (999.9 Four Nine Fine) Perfect Fineness : 0.6180339^(1/(19*(365.25)^0.6180339)) = 0.999 (24 Karat)
For Silver Ten
Minimum Fineness : 0.414213562^(1/19) = 0.955 (Britannia Silver) Theoretical Maximum Fineness : 0.414213562^(1/(19*365.25)) = 0.9999 (999.9 Four Nine Fine) Perfect Fineness : 0.414213562^(1/(19*(365.25)^0.414213562)) = 0.996 (23.9 Karat)
For Copper Sen
Minimum Fineness : 0.302775638^(1/19) = 0.940 (Coinage Bronze) Theoretical Maximum Fineness : 0.302775638^(1/(19*365.25)) = 0.9999 (999.9 Four Nine Fine) Perfect Fineness : 0.302775638^(1/(19*(365.25)^0.302775638)) = 0.99 (990 Two Nine Fine)
For recapitulation :
| Minimum Fineness | Perfect Fineness | Theorical Maximum Fineness | |
| x^(1/19) | x^(1/19*365.25^x) | x^(1/19*365.25) | |
| Gold Ren (0.6180…) | 975 | 999 | 9999 |
| Silver Ten (0.4142…) | 955 | 996 | 9999 |
| Copper Sen (0.3027…) | 940 | 990 | 9999 |
Geometry :
The geometry of the coin can be any geometry, anyone can design his own coins. The only constraint is that the geometry must make the fineness of a coin verifiable by any person with only his 5 senses in few second and in a instant by using Ren's intinct if the person is a Nen user (Ren will be later introduced in detail by Pakka M. Jodinshi).
A verification can be by feeling the weight, dimension, shape, texture, color/light frequency, sound frequency, resiliance by hand pressure for Gold Ren, sound frequency for Silver Ten and bending for Copper Sen.
Our proposal for such a geometry is usage of Gyroids : For Gold Ren : A Gyroid with very thin Walls. For Silver Ten : A Double Gyroid with thin Walls. For Copper Sen : A Double Gyroid with Thick walls.
You can see bellow a simple rendering of the coins in their respective geometry

The more fineness a geometry can verify the more optimal it is. We can see the geometry searching as a Optimization Problem. So This proposition can be optimized by any Deep Learning Machine with our proposal as a starting point. That make the coin with time more secure and more difficult to counterfeit in fineness.
Also with the gyroid geometry, will make fingerprint analysis on the coins and tracing it's previous owners nearly impossible. This will make it the first anonymous physical coin.
Minting :
The minting is done by 3D Metal Printing the coin with the right fineness powder.
In the future, with evolution of Affordable Desktop Metal Printer, anyone will be able to download the optimal 3D model of the coins and begin minting blocks anywhere on earth.
To make the coin independent of a central minting. The Gold Ren and Silver Ten coins need to be free from signature, marks, names, information like "1 REN", "12 Ren", "4.00g", "48.00g", "999 pure gold", "Minted in Nowhereland". The identification of those coin is made by feeling it's grasshopper geometry, color, design, weight measure, mechanical characteristic with hand pressure, therefore It dont need any marking.
Those coins is trust-less. You dont have to trust a specific marking on the coin to verify it.
This will make it the first trustless decentralized precious metal coins.
And those are Gold Ren, Silver Ten and Copper Sen.

Golden Yen, Silver Ken and Bronze Jen are 3-in-1 cryptocurrency made respectively from The Golden Mean 1.618…, The Silver Mean 2.414… and The Bronze Mean 3.302… where each coin have a fixed average fineness (fee) and it's weight in grams (mined) and blocksize is adjusted by the network so each coin is equal in value to its respective physical coin. It decentralization is assured by the process of "Data Minting".
Process.
The process of the system of Gold Ren, Silver Ten and Copper Sen are 3 phases : Mining of precious metal, Minting it to Blocks with a predefined fineness. And from the Block, coins are issued and transacted by the users of the coins.
For Golden Yen, Silver Ken and Bronze Jen the 3 phases are inversed. First the users make transactions, then Minters verify transactions if the coins transacted have the correct fineness (fees) and assemble them to blocks with a predefined size and density then give it to Miners. And then Miners mine the block and new grams get created according to the Metallic Fibonnaci Sequence of the coin (The Golden Mean 1.618…, The Silver Mean 2.414… or The Bronze Mean 3.302…).
Blockchain.
In the year 2008, Satoshi Nakamoto introduced the Blockchain which use the process of transacting and mining to create a decentralized electronic currency. The first implementation of Blockchain was Bitcoin made by Satoshi himself and with time alternative coins emerged from it, we take as exemple Litecoin and Dogecoin.
The system of Golden Yen, Silver Ken and Bronze Jen use the same concept of a system made with Bitcoin, Litecoin and Dogecoin. Where Bitcoin a good store of value but hard to transact, Litecoin easy to transact but hard to microtransact and Dogecoin easy to mircotransact but hard to store a value.
For Golden Yen, Silver Ken and Bronze Jen, their blockchain characteristic will be as fellow :
| Golden Yen | Silver Ken | Bronze Jen | |
| Metallic Order | 1 | 2 | 3 |
| Block Size (initial) | 4 mb | 3 mb | 2 mb |
| Block Time | 15 min | 5 min | 2.5 min |
Supply.
For Bitcoin, the supply is halved for every static 210000 blocks, which make it with limited supply. But for Golden Yen, Silver Ken and Bronze Jen, the halving is variable and done after every number of the Mettalic Fibonnaci Sequence (U(N+1) = M*U(N) + U(N-1) where U(0) = 1 and U(1) = 1).
For Golden Yen, the sequence of the Golden Mean (1.618…) is the simple Fibonnaci sequence of U(N+1) = U(N) + U(N-1) where M = 1 and the limit of U(N+1)/U(N) to infinity is 1.618… .
For a initial block reward of 2520. The supply of Golden Yen will be as fellow :
| Sequence | Block's number | Block reward | Blocks Reward | Supply |
| 1 | 1 | 2520,0000 | 2520,00 | 2520,00 |
| 1 | 2 | 1260,0000 | 1260,00 | 3780,00 |
| 2 | 3 | 630,0000 | 1260,00 | 5040,00 |
| 3 | 5 | 315,0000 | 945,00 | 5985,00 |
| 5 | 8 | 157,5000 | 787,50 | 6772,50 |
| 8 | 13 | 78,7500 | 630,00 | 7402,50 |
| 13 | 21 | 39,3750 | 511,88 | 7914,38 |
| 21 | 34 | 19,6875 | 413,44 | 8327,81 |
| 34 | 55 | 9,8438 | 334,69 | 8662,50 |
| 55 | 89 | 4,9219 | 270,70 | 8933,20 |
| 89 | 144 | 2,4609 | 219,02 | 9152,23 |
| 144 | 233 | 1,2305 | 177,19 | 9329,41 |
| 233 | 377 | 0,6152 | 143,35 | 9472,76 |
| 377 | 610 | 0,3076 | 115,97 | 9588,74 |
| 610 | 987 | 0,1538 | 93,82 | 9682,56 |
| 987 | 1597 | 0,0769 | 75,90 | 9758,46 |
| 1597 | 2584 | 0,0385 | 61,41 | 9819,87 |
| 2584 | 4181 | 0,0192 | 49,68 | 9869,55 |
| 4181 | 6765 | 0,0096 | 40,19 | 9909,74 |
| 6765 | 10946 | 0,0048 | 32,52 | 9942,26 |
| 10946 | 17711 | 0,0024 | 26,31 | 9968,57 |
| 17711 | 28657 | 0,0012 | 21,28 | 9989,85 |
| 28657 | 46368 | 0,0006 | 17,22 | 10007,07 |
| 46368 | 75025 | 0,0003 | 13,93 | 10020,99 |
| 75025 | 121393 | 0,0002 | 11,27 | 10032,26 |
| 121393 | 196418 | 0,0001 | 9,12 | 10041,38 |
For a block time of 15 min, the supply will reach 10000 after 1 year. The reward will reach 4 decimals and total supply 10041,38 after 5 years and 8 decimals rewards with a total supply of 10077,54 after 3000 years. (The limit supply is 2520*4 = 10080)
Which mean at the first year 99% of the coin will be mined, 0.5% is added after 4 years. And for a period of 3000 years only 0.475% will be added to the supply. This supply sequence is a good equivalent to gold as a store of value... but not the greatest. Gold mining is probabilistic and the reward decrease smoothly when mining it which make it robust to manipulation and monopole.
To apply the propriety of smoothness. The halving sequence is smoothed as fellow :
Raw_Reward(N) = 2520*(1/2)^(log(N)/log(1.6180339)) where N is the block number
And to make it probabilistic, we add a random variable V with a Geometrical Normal Distribution where the geometrical average is 1 :
V = 1.6180339^(PPF(Random(), 0, 1))
Then the reward will be :
Reward(N) = Raw_Reward(N)*V
To simulate this supply we will use python :
import math
import random
from scipy.stats import norm
import matplotlib.pyplot as plt
def simulate(metal,block_time,period):
History = []
Raw_Reward = 2520
Supply = 0
Ratio = (metal+math.pow(metal*metal+4,0.5))/2.
for i in range(int(Period*60/block_time)):
V = math.pow(Ratio,norm.ppf(random.random(),0,1))#qrng.get_double(),0,1)) for Quantum Random Number Generator
Supply = Supply + Raw_Reward*V
for j in range(int(block_time*2)):
History.append(Supply)
Raw_Reward = 2520*math.pow(0.5,(math.log(i+1))/math.log(Ratio))
print "({}, {}, {}) {}/{}\r".format(metal,block_time,period,i+1,int(Period*60/block_time)),
print "({}, {}, {}) {}/{} Done\r".format(metal,block_time,period,i+1,int(Period*60/block_time))
return History
Period = 365
Golden_Yen = simulate(1,15,Period)
Silver_Ken = simulate(2,5,Period)
Bronze_Jen = simulate(3,2.5,Period)
#Fiat_Dollar = simulate(607,1,Period)
plt.plot(Golden_Yen,'y')
plt.plot(Silver_Ken,'b')
plt.plot(Bronze_Jen,'r')
#plt.plot(Fiat_Dollar,'g')
print "Golden Yen Supply : {}".format(Golden_Yen[-1])
print "Silver Ken Supply : {}".format(Silver_Ken[-1])
print "Bronze Jen Supply : {}".format(Bronze_Jen[-1])
#print "Fiat Dollar Supply : {}".format(Fiat_Dollar[-1])
print "KEN/YEN : {}".format(Silver_Ken[-1]/Golden_Yen[-1])
print "JEN/KEN : {}".format(Bronze_Jen[-1]/Silver_Ken[-1])
print "JEN/YEN : {}".format(Bronze_Jen[-1]/Golden_Yen[-1])
#print "YEN/USD : {}".format(Fiat_Dollar[-1]/Golden_Yen[-1])
#plt.yscale('log')
plt.show()
The output :
(1, 15, 365) 1460/1460 Done
(2, 5, 365) 4380/4380 Done
(3, 2.5, 365) 8760/8760 Done
Golden Yen Supply : 7926.14910662
Silver Ken Supply : 95840.1695458
Bronze Jen Supply : 512948.698107
KEN/YEN : 12.0916435278
JEN/KEN : 5.35212636348
JEN/YEN : 64.7160041032
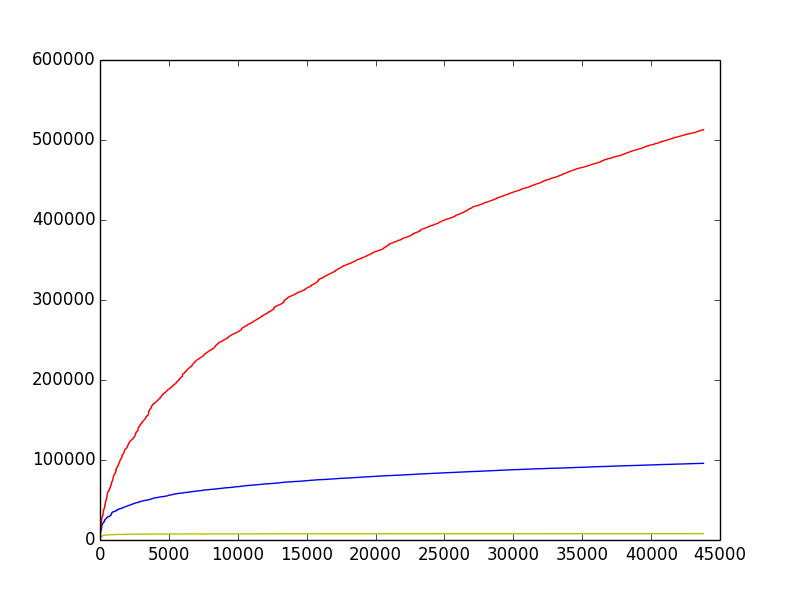
In the graph, we see that even with a random probabilistic reward the supply is very smooth for the three coins. There is no perturbation in any of the 3 coins. Golden Yen converge rapidly, the Silver Ken increase with a slow logarithmic pace and Bronze Jen with a fast logarithmic pace.
For comparaison, we added Fiat Dollar with the metallic number 607 calculated from width (6.6294 cm) and thickness (0.010922 cm) of a paper dollar and it give a ratio 6.6294/0.010922 = 606.976744186 and a metallic number (606.976744186^2-1)/606.976744186 = 606.975096676, which is 607. And we got this output :
(1, 15, 365) 1460/1460 Done
(2, 5, 365) 4380/4380 Done
(3, 2.5, 365) 8760/8760 Done
(607, 1, 365) 21900/21900 Done
Golden Yen Supply : 10294.6749455
Silver Ken Supply : 86696.8561897
Bronze Jen Supply : 538068.805184
Fiat Dollar Supply : 2.92936875856e+14
KEN/YEN : 8.42152439478
JEN/KEN : 6.20632429861
JEN/YEN : 52.2667114827
YEN/USD : 28455184588.9
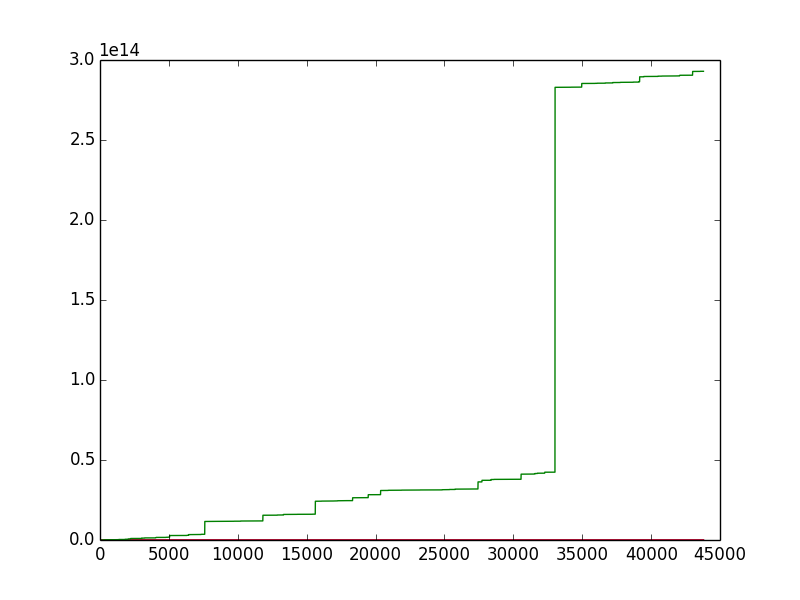
In the chart, we can see only the Fiat Dollar, its supply have increased in a massive scale that the 3 coins supply are inexistant. And we can see that the Dollar increase like a Devil's Staircase Function, where every small jump can be interpreted by a Quantitative Easing from the Federal Reserve or a Central Bank. And after the supply reach 40 Trillion Dollar, it jumped in a instant 700% to 292 Trillion Dollar which is no doubt can be interpreted as the HyperInflation of the currency.
Anti-Prime Decentralization
Anti-Primes are numbers with the most divisors. Contrary of Primes numbers which they appear randomly in the integer set. Anti-Primes are very predictable, it's possible to generate them with this simple algorithm in python :
import math
Primes = [2]
Anti_Primes = [1]
Exponents = [0]
N = 10
for i in range(N) :
Min_x = float('inf')
Min_j = 0
for j in range(len(Primes)) :
if Exponents[j-1]>Exponents[j] or j == 0:
x = math.log(Primes[j])/math.log(1./(Exponents[j]+1.)+1.)
if x < Min_x :
Min_x = x
Min_j = j
Exponents[Min_j] = Exponents[Min_j] + 1
if Min_j + 1 == len(Primes) :
Exponents.append(0)
Next_Prime = Primes[len(Primes)-1]+1
j = 0
while (Primes[j]*Primes[j]<=Next_Prime) :
if Next_Prime%Primes[j] == 0:
j=0
Next_Prime = Next_Prime + 1
else:
j = j + 1
Primes.append(Next_Prime)
Anti_Primes.append(Anti_Primes[-1]*Primes[Min_j])
print "{}/{}\r".format(i+1,N),
print "{}/{}\r Done".format(i+1,N)
print Anti_Primes
As primes are used to decompose a number to product of prime numbers. It's possible to use Anti-Primes to decentralize a number to sum of Anti-Primes numbers very fast.
In this exemple we decentralize the message "Hello World!" to a list of anti-primes, shuffle the list then centralize them again to restore the message, in this example we used Python 3 instead of normal Python:
import math
import random
Primes = [2]
Anti_Primes = [1]
Exponents = [0]
def generate_antiprimes_for(Number):
while (Anti_Primes[-1]< Number):
Min_x = float('inf')
Min_j = 0
for j in range(len(Primes)) :
if Exponents[j-1]>Exponents[j] or j == 0:
x = math.log(Primes[j])/math.log(1./(Exponents[j]+1.)+1.)
if x< Min_x :
Min_x = x
Min_j = j
Exponents[Min_j] = Exponents[Min_j] + 1
if Min_j + 1 == len(Primes) :
Exponents.append(0)
Next_Prime = Primes[len(Primes)-1]+1
j = 0
while (Primes[j]*Primes[j]<=Next_Prime) :
if Next_Prime%Primes[j] == 0:
j=0
Next_Prime = Next_Prime + 1
else:
j = j + 1
Primes.append(Next_Prime)
Anti_Primes.append(Anti_Primes[-1]*Primes[Min_j])
def decentralize(Number) :
#print("Decentralizing Number :",Number)
i = len(Anti_Primes)
Result = []
while i > 0:
if Anti_Primes[i-1] <= Number :
Number = Number - Anti_Primes[i-1]
Result.append(i)
while Number < Anti_Primes[i-1] and i>0:
i = i - 1
return Result
def centralize(Fact_Number) :
Sum = 0
for i in range(len(Fact_Number)) :
Sum = Sum + Anti_Primes[Fact_Number[i]-1] #Centralizing code
return Sum
def string_decentralize(Message):
Int_Code = int.from_bytes(Message.encode(),byteorder='big')
generate_antiprimes_for(Int_Code)
Fact_Number = decentralize(Int_Code)
return Fact_Number
def string_centralize(Fact_Number):
Expan_Number = centralize(Fact_Number)
Code = Expan_Number.to_bytes(256, byteorder='big')
Message = Code.decode()
return Message
Send_Message = "Hello World!"
Fact_Number = string_decentralize(Send_Message)
#random.shuffle(Fact_Number)
Recieved_Message = string_centralize(Fact_Number)
print("Message :", Send_Message)
print("Factors :", Fact_Number)
print("Assembled Message :", Recieved_Message)
Result :
Message : Hello World!
Factors : [32, 31, 31, 31, 31, 31, 31, 31, 31, 29, 29, 29, 29, 29, 29, 29, 29, 29, 29, 29, 29, 29, 29, 29, 29, 29, 29, 29, 29, 29, 29, 29, 29, 29, 29, 29, 29, 29, 29, 29, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 25, 25, 25, 25, 25, 25, 25, 25, 25, 25, 25, 25, 25, 25, 25, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 22, 21, 21, 21, 21, 21, 21, 21, 21, 20, 20, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 18, 17, 17, 17, 17, 17, 17, 17, 17, 17, 17, 17, 17, 17, 17, 17, 17, 17, 17, 17, 16, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 13, 12, 10, 10, 10, 10, 10, 9, 9, 9, 9, 9, 7, 6, 5, 2, 2, 1]
Assembled Message : Hello World!
Traveler Salesman Problem
In the last exemple, we have decentralized the message "Hello World!" into list of Anti-Primes:
[32, 31, 31, 31, 31, 31, 31, 31, 31, 29, 29, 29, 29, 29, 29, 29, 29, 29, 29, 29, 29, 29, 29, 29, 29, 29, 29, 29, 29, 29, 29, 29, 29, 29, 29, 29, 29, 29, 29, 29, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 25, 25, 25, 25, 25, 25, 25, 25, 25, 25, 25, 25, 25, 25, 25, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 23, 22, 21, 21, 21, 21, 21, 21, 21, 21, 20, 20, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 18, 17, 17, 17, 17, 17, 17, 17, 17, 17, 17, 17, 17, 17, 17, 17, 17, 17, 17, 17, 16, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 13, 12, 10, 10, 10, 10, 10, 9, 9, 9, 9, 9, 7, 6, 5, 2, 2, 1]
If we compact the list as (index, multiplicator) we will get a more compacted list of points :
[(32, 1), (31, 8), (29, 31), (28, 28), (25, 15), (24, 37), (23, 36), (22, 1), (21, 8), (20, 2), (19, 13), (18, 1), (17, 19), (16, 1), (15, 11), (14, 16), (13, 1), (12, 1), (10, 5), (9, 5), (7, 1), (6, 1), (5, 1), (2, 2), (1, 1)]
When we plot the points into a chart we will get this :
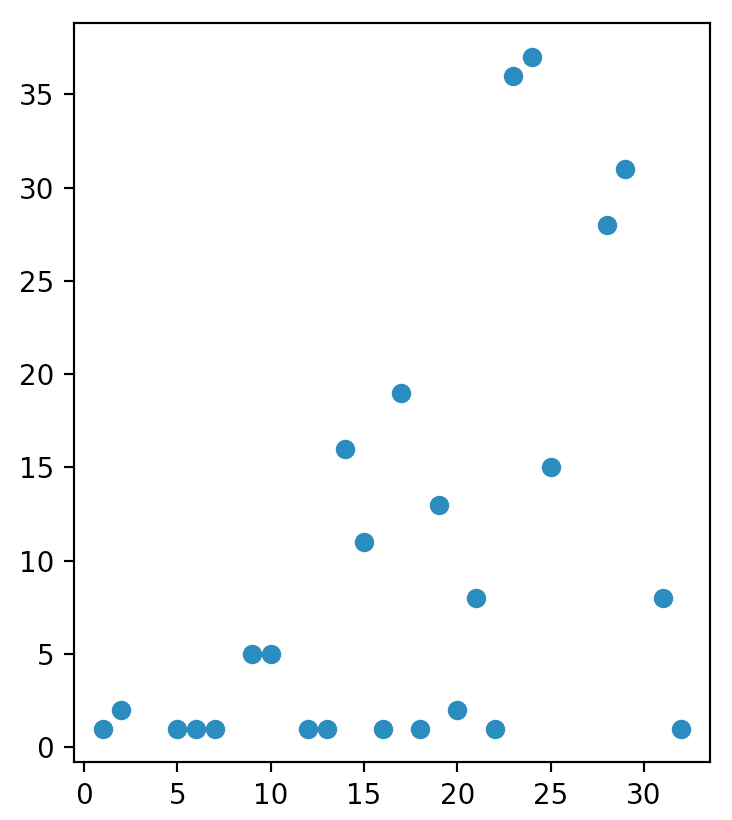
And to encode them the most optimal way whe need, we will try to order them as such the distance to travel each point is optimal.
… (Under Research and Development)
Anti-Prime Encodage
To encode the anti-prime list, we will try to encode only the minimum information from the list. Because the anti-primes are permutable, The first idea is to encode it as a two element list, those element are :
The index Multiplicator of the index
And to make it more compact. The index is coded as the increment of the previous index :
The increment to get this index Multiplicator of the index
For the multiplicator of an index, cant be bigger than the ratio between the anti-prime of the index and the anti-prime next to it. For exemple, the index 6 is the anti-prime 360 and the anti-prime next to it is 2520. The ratio is 2520/360 = 7, which mean that the multiplicator of 360 can never be bigger than 7 and can only be 1, 2, 3, 4, 5 or 6. Then the list will be :
The increment to get this index Multiplicator of the index (encoded in anti-prime(index +1)/anti-prime(index))
and to encode the increment, we will add a third element encoded in a fixed 5 bits :
The size of the increment (encoded in 5 bits) The increment to get this index (encoded in the size of the increment) Multiplicator of the index (encoded in anti-prime(index +1)/anti-prime(index))
… (Under Research and Development)
Data Minting
By modifying the code of Anti-Prime encoding it's possible to make a process similar to the Proof-of-Work process. By permuting the anti-primes list and try to find a combinaison which the Anti-Prime decentralization of the encoded message have lesser element than the Anti-Prime decentralization of the message.
… (Under Research and Development)
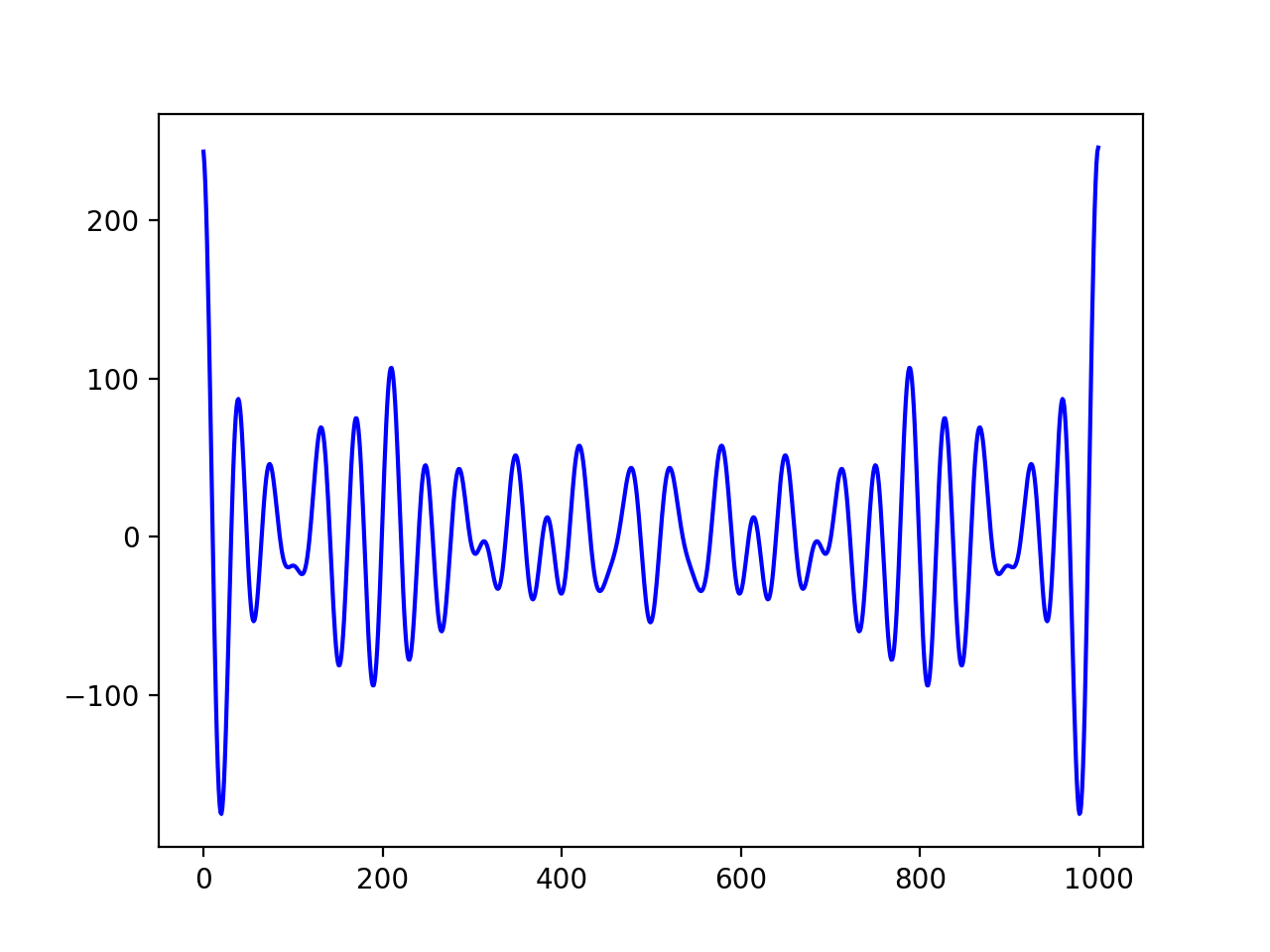
Anti-Primes Inverse Fourier Transform Signal
For wireless frequency communication of minted blocks between nodes.
(Exemple of transforming "Hello World!" into this Anti-Primes Signal)
(Exemple of transforming the popular 69 words of "Lorem Ipsum…est laborum." into this Anti-Primes Signal)
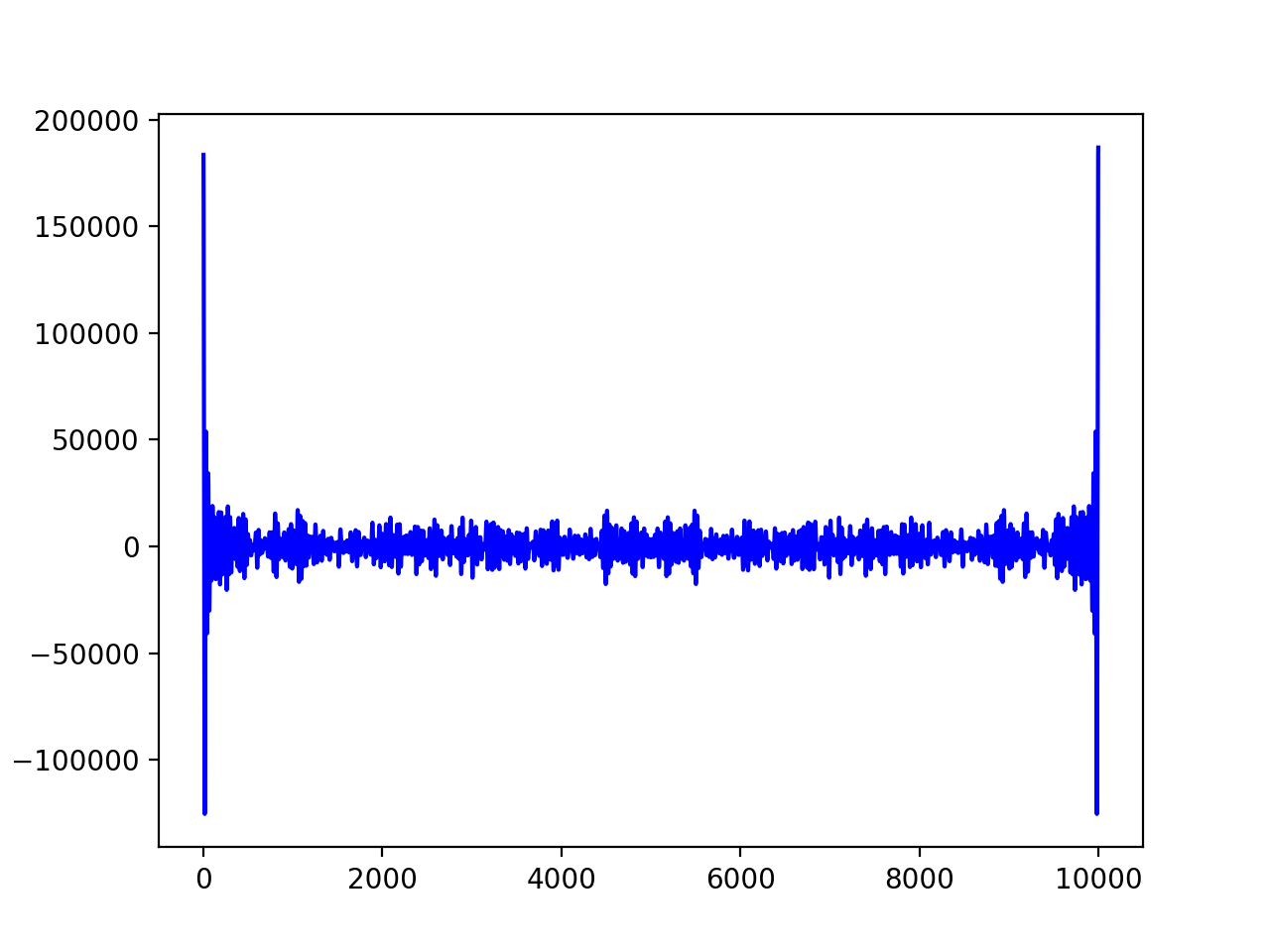
… (Under Research and Development)
Block Minting and Block Density
If we do the same thing to blocks, it's possible to mint a big amount of transaction into a limited size. This is were the work of Minters comes in.
The work of the Minters, is minting a block until it reach the density predefined by the network. And the density is adjusted in a way the network mint a block each block's time. (15min for Golden Yen, 5min for Silver Ken and 2.5min for Bronze Jen)
For a network with only 1 single minter. The minter first collect transactions in a block until it reach the size limit. Then begin to mint by making blows (Many Mint attempt) . If a blow made a space in the block. he add transaction to cover the space. And then continue to make blows again. and the process repeat and repeat. Until the block reach the density of the network. Then the minter hand over it to miners.
For a network with many minters. The minters of the whole network collaborate to mint a single block. Where all Minters make blows in parallel on the same block and each minter uses a unique hammer that if one made a lucky blow and made a space in the block, every one will know for sure that he is the one who made it. And he can claim a share of the fees of the block.
To achieve this, the initial block need to be decentralized in Anti-prime list. Where all minters have the same copy. Each minters try to make a blow of Shuffle it. Signed it. And Decentralized it. If after a blow a space is made. Then he add a minter transaction that give some of the fee of the block he minted to the next one who will make a blow and send the block to other minters. Then cover the space with transactions and repeat the blows.
Then the other minters receive many blocks with space from other minters, And they just need to chose the more danse block that have the higher fee. And cover the space by new transactions then they do the same to it by making blows (Shuffle it. Signed it. And Decentralized it). If one have made a space is made, he add a minter transaction then send it to other minters.
And this process repeat until the block achieve the density. And Miners receive the block.
Anti-Primes Metallic Hash
For Metallic Signature and Mining.
… (Under Research and Development)
Block Mining and Block Difficulty
When minting is a collaboratif. Collaboration to compress transactions into a block. Mining is a competitive.
The work of the Miners is to receive the final Minted block, then mined it to the blockchain. To do this they need to solve a mathematical problem. And when someone find a solution he will get rewarded by newly created grams.
… (Under Research and Development)
Quantum Searching
Usage of Randomness Expansion of Quantum Random Number Generator in Minting and Mining.
…(Under Research and Development)
Block resizing.
The Block size of Golden Yen, Silver Ken and Bronze Jen begin as 4mb, 3mb and 2mb. Then if there is a resize of a block by adding 50%. The size will be 6mb, 4.5mb and 3mb. The proportion between the three need to be the same.
The Blocks need to be resized in a way which the geometrical average of the % in fee is close to the standard average % fee of the coin.
For exemple, with the block size of Golden Yen, Silver Ken and Bronze Jen are 4mb, 3mb and 2mb.
The standard average % fee of Golden Yen, Silver Ken and Bronze Jen are 0.1%, 0.4% and 1%.
We calculate the geometric average of % fee from previous blocks in fibonnaci halving weight. And we found the geometrical average 1%, 2% and 3%.
From the formule x^(1/19*365.25^x^p), we need to find p which x^(1/19*365.25^x^p) is the geometric average.
p = log(log(log(x)/(19*log(y)))/log(365.25))/log(x)
For 1% of Golden Yen, we have p = log(log(log(0.6180339)/(19*log(1-0.01)))/log(365.25))/log(0.6180339) = 3.85 For 2% of Silver Ken, we have p = log(log(log(0.41421356)/(19*log(1-0.008)))/log(365.25))/log(0.41421356) = 2.22 For 3% of Bronze Jen, we have p = log(log(log(0.30277563)/(19*log(1-0.02)))/log(365.25))/log(0.30277563) = 1.75
The factor P need to be the metallic weighted geometric average of the three.
P = ((3.85^0.6180339)*(2.22^0.41421356)*(1.75^0.30277563))^(1/(0.6180339+0.41421356+0.30277563)) = 2.71402584819
Then the 3 bloc size need to be multiplied by 2.71 which will get. 10.84mb, 8.13mb and 5.42mb.
To explain this process more. The monetary system is made into 3 layers of money. The best money is gold, which is at the top of the 3 layers. It has the best store of value, it can buy a house, a car, computer, a phone but it can't buy an everyday transactions like a breakfast. To pay for such transaction, the person need to go to the layer under it, the silver layer and then use some of the silver to pay for a breakfast. But the same as the gold layer, the silver layer can't buy a Chewing-gum. He need to go to the bottom layer the bronze layer, and then use some of the bronze to pay for a Chewing-gum.
In the exemple, the Golden Yen got from 0.1% to 1%, which mean the network is full. If it was an independent network resize of x3.85 is needed. But the formula have give x2.71. Because Silver Ken and Bronze Jen are less full. When the resize is done the three network will be 1.42, 0.82, 0.64. Then the 0.42 left of Golden Yen have to go to the layers below it, because is cheaper.
But in practice, the resizing need to be smooth to avoid any disturbance in the fees and the network. So the resize need to be done at every block.
In practice the block size will increase smoothly if average % fee of transaction are higher than the standard. and decrease smoothly if it's lower.
Fineness (Transaction fees)
The fineness of Golden Yen, Silver Ken and Bronze Jen are the same as the Gold Ren, Silver Ten and Copper Sen. The fineness are as fellow :
| Minimum Fineness | Average Fineness | Maximum Fineness | |
| Golden Yen (0.6180…) | 975 | 999 | 9999 |
| Silver Ken (0.4142…) | 955 | 996 | 9999 |
| Bronze Jen (0.3027…) | 940 | 990 | 9999 |
In transaction fee, it will be as fellow :
| Maximum % in Fee | Average % in Fee | Minimum % in Fee | |
| Golden Yen (0.6180…) | 2.5% | 0.1% | 0.01% |
| Silver Ken (0.4142…) | 4.5% | 0.4% | 0.01% |
| Bronze Jen (0.3027…) | 6% | 1% | 0.01% |
Any transaction that have a transaction fee bigger than the maximum % in fee or smaller than the minimum % in fee of the amount are rejected.
For exemple a Golden Yen transaction of 99 coin with 1 coin in fee have a fee of 1/(99 +1) = 1% which is accepted. Therefore if the fee is less than 0.01% or bigger than 2.5% it will be rejected. And this where made to avoid fee spamming and fee price manipulation.
In bitcoin the fee is set by the sender. But in our case, the fee is set by the receiver. For exemple a merchant can set a minimum fineness a coin when generating an address. For exemple an merchant address for 100 Yen 9995 pure or 900 Ken 9998 pure or 30000 Jen (9999 Pure).
Therefore in the transaction history of the wallet you can see. The fineness of every coins recieved and sended.
Grams unit :
For Golden Yen, the first block reward is have the probabilistic mean of 2520 unit. Then after it the will decrease smoothly by approximately halving on each number on the fibonacci sequence.
For bitcoin the smallest reward is a satoshi which is 0.00000001 BTC. But for our case and to add some precision, we will make it one Pico, which is 0.000000000001
Then the first reward will be 2520000000000000 unit.
If we define this unit system : XXX gigatonnes XXX megatonnes XXX kilotonnes XXX tonnes XXX kilograms XXX grams XXX milligrams.
Or in short : XXXgt XXXmt XXXkt XXXt XXXkg XXXg XXXmg.
Then the first reward will have a probabilistic mean of 2mt 520kt.
Coin's weight :
The same as a Golden Ren have 4.00 grams of gold in a predefined 999 fineness. The weight of a Golden Yen coin must be predefined and change automatically in way that will always have a fineness of 999 or a fee of 0.1%.
We need to calculate the metallic average from previous blocks. and divide it by the geometrical averages of the % in fee. For exemple an golden average fee of 6t, and the geometrical average is 0.11% will make the weight of a coin is 6/0.1% = 5mt 454t.
And the averages from previous bloc is calculated by calculating the normal average of each previous block (B(-1),B(-2),B(-3),B(-4),….), then do the weighted average according to the halving in Fibonacci sequence of the metallic order :
(B(-1) + B(-2)/2 + B(-3)/2 + B(-4)/4 + ….)/(1 + 1/2 + 1/2 + 1/4 + 1/4 + 1/4 + 1/8 + 1/8 + 1/8 + 1/8 + 1/8 + 1/16 + 1/16 + 1/16 + 1/16 + 1/16 + 1/16 + 1/16 + 1/16…)
The same with the weighted standard deviation.
Then with the average and the standard deviation. We can calculate the metallic average where the area is of the normal distribution is equal to the metallic mean.
For Golden Average is Average + 0.3*SD For Silver Average is Average - 0.216*SD For Bronze Average is Average - 0.515*SD
This make the Golden Yen unit of coin more divisible than Silver Ken and Bronze Jen.
For the smallest fraction of the unit is where it's maximal fee is equal to the minimal fee of the standard weight coin which is Minimal % Fee / Maximal % Fee.
For Golden Yen is 0.0001/0.025 = 0.004 YEN For Silver Ken is 0.0001/0.045 = 0.002 KEN For Bronze Jen is 0.0001/0.025 = 0.001 JEN
Any transaction with amount smaller than those fractions of the standard coin weight is rejected. Because is either they have a fee higher than the maximum or the fee is too low and can overload the network.
At the first blocks, the weight of a coin will be heavy then the more user will come and make transactions the lighter the coin will be. And in the other way the more the fee the heavier the coin, the less the fee the lighter coin. In short a coin will be independent of the fee. A coin will always have the same fineness.
In this way it will make possible to value the coins. By setting prices of good and services to it without carrying about volatility.
And it even possible to set 1 YEN = 1 REN. And the Golden Yen Network will by itself find the perfect standard weight of a Golden Yen Coin in a way which the value of 1 Gold Ren is the same as 1 Golden Yen.
And also if there is a exchange consensus of 1 YEN = 1 REN (4.00g Gold), 1 KEN = 1 TEN (3.00g Silver) and 1 JEN = 1 SEN (2.00g Copper). It will be hard for any other Alternative cryptocurrency to compete with the consensus. And it will bring everyone to one single cryptocurrency which will be the Gold Ren/Yen, Silver Ten/Ken and Bronze Sen/Jen.
Mining Order and start
The mining wil start with Bronze Jen. Then after a period, Silver Ken will start to be mined. Then after a period the last Golden Yen.
Like bitcoin, when Bronze Jen will be first mined it will be only in few nodes, becaus it's the early start and there is no commerce or service that accept this new crypto. But when the Bronze Jen usage and community will grown more nodes will join the network. And because it supply is fast logarithmic. The early miners wont have a monopoly over the Jen grams.
After a period of growth in usage, it will be enough nodes to ensure fairness when the new Silver Ken will start to be mined. And then after a period the last Golden Yen will be mined.
The condition which the Silver Ken and Golden Yen will start to be mined is determined by the size of the Raw Reward defined earlier.
For Bronze Jen, the first Raw Reward is 2520 and reduce overtime according to the Bronze Ratio. When the raw reward is less than 1 is the condition to start the mining of Silver Ken.
We know the equation to calculate the raw reward for a block N :
Raw_Reward(N) = 2520*(1/2)^(log(N)/log(3.302775)) where N is the block number
When the raw reward is equal to 1 :
1 = = 2520*(1/2)^(log(N)/log(3.302775))
N = 3.302775^(log(2520)/log(2))
N = 729327.47
So it need 729328 blocks to have a reward less than 1. And we know that Bronze Jen block time is 2.5 min. The time is 729328*2.5/(60*24*365) = 3.46 years. So the only Bronze Jen will be mined for 3 and half years before Silver Ken start to be mined.
If we do the same for Silver Ken :
N = 2.41421^(log(2520)/log(2))
N = 21137.91
Silver Ken need 21138 blocks to have a reward less than 1. We know Silver Ken block time is 5 min. So the time is 73 = 2.44 months. Then 2 and half months after the start of Silver Ken is when Golden Yen will start to be mined.
| Bronze Jen | Silver Ken | Golden Yen | |
| Time to start | 0 | 3.5 Years | 3.5 Years + 2.5 Months |
Exchange rate calculation :
With the variation of the coins weight of the electronic coins, we can link it to the physical coins and set 1 YEN = 1 REN, 1 KEN = 1 TEN and 1 JEN = 1 SEN. But how to solve the exchange rate between physical coins, for example Gold Ren and Silver Ten without the using of a centralized exchange marketplace.
To solve this problem, we will use the same electronic coins Golden Yen, Silver Ken and Bronze Jen.
First we need to find a way to calculate the exchange rate between the 3 cryptographic coins only from their blockchain.
Because each wallet's private key, can send any of the 3 type of coin, and a wallet public address can receive any of the 3 coins.
We can filter transactions from the 3 blockchains, and find if there is two transactions from two different blockchain (for example a transaction for the Golden Yen Blockchain, and the second from the Silver Ken Blockhain) where the sender of the first transaction is the receiver of the second, and the receiver of the first is the sender of the second.
Example :
1 Transaction in Golden Yen's Blockchain : Sender : Person A (from multiple public address that received coins) Receiver : Person B (1827b9691) Amount : 5 Coins left to : Person A (f551bb079)
1 Transaction in Silver Ken's Blockchain : Sender : Person B (from multiple public address that received coins) Receiver : Person A (f551bb079) Amount : 60 Coins left to : Person B (1827b9691)
This mean that Person A (with public address: 1827b9691) have exchanged 5 YEN for 60 KEN with Person B (with public address: f551bb079). So the rate of that exchange transaction is 12 KEN/YEN.
As you can see, with the use of the same public addresses, we can find all the exchange transactions on two different blockchains. And with those exchange transactions we can calculate the mean exchange rate in a point of time without the need of a centralized exchange marketplace.
And when we the exchange rate of each of the 3 electronic coins are calculated and stabilized. (KEN/YEN, JEN/YEN, JEN/KEN). And we already have 1 REN = 1 YEN, 1 TEN = 1 KEN and 1 SEN = 1 JEN.
We have can know the exchange rate of each of the physical coins TEN/REN, SEN/REN and SEN/TEN just from the Blockchain. And with that not only physical coins are merged with the electronic, but also the 3 type Gold, Silver and Copper are merged into one indepedent unit of value.
And now setring price of goods and services will be easy without worrying about which one physical or electronic, or in Gold coin or Silver coin or Copper coin, because when the weights and exchange rate are set, they are all the same.
And those are Golden Yen, Silver Ken and Bronze Jen.

Y-Network, K-Network and J-Network are 3 channel factories build on top fo the Golden Yen, Silver Ken and Bronze Jen. Where anyone can meltdown their coins to grams and stream it to anyone in the network. It decentralization is assured by the geographic distribution of Zen towers nodes.
Channel factories
Channel factories is a solution for the scalability problem of bitcoin. Made by Conrad Burchert, Christian Decker, and Roger Wattenhofer. It propose 2 layers on top of the cryptocurrency. Where anyone can enter the system with one transaction on the blockchain and anyone can open a channel with anyone and stream bitcoin.
In our case the channel factories is an electronic factory where anyone can meltdown their coins and stream pure grams to anyone in the factory and at the end remint it to standard coins.
And those are Y-Network, K-Network and J-Network
...
(Under Research and Development)
Zen Towers
Zen Tower, is a unit that offer 5G/Wifi internet, Channel Channel factory node routing, Mining/Minting, 3D Minting, God's Blocks Distribution and exchange between the 9 types of money. But the most importantly is it offer the exchange between an electronic money to physical money (to Gold Ren, Silver Ten and Copper Sen). Which will make it distributed across the land and avoid any centralization of nodes.
The channels between Zen Towers need to be in a Hexagonal geometry. Where every Tower have 3 YKJ-channels to towers near to it. (3 Y-Network channel, 3 K-Network channel and 3 J-Network channel). And people open channels to the near Zen tower for physical/electronic/routing exchanges.
Tesla & Zen Towers
Yet another technology that can be merge with Zen towers, are Nikola Tesla's World Wireless System Towers (Click to enlarge)
Tesla towers are towers that can offer free energy and information transmission wirelessly through the whole planet. Including that technology in Zen towers, we can achieve a world wide system that can distribute energy, internet and money across everyland land.
Nen Machines
Nen machines are the next generation machine/computer/smartphone that use memristors, optic fiber and mass processing units as computers. Hewlett Packard Corporation are aleardy made research about this type of machines, calling it "The Machine". But still no commercial use was made.
This new type of machine, will exceed the current computer technologies in memory, storage and processing power. And with Zen towers and it distribution of energy and internet and money. Its possible to have many application of it.
For exemple in the Nen devices, we can build the 3-in-1 cryptocurrencies with the 3 YKJ-channels network on the OS kernel of the device. And on top of that OS build a decentralized and anonymous internet protocol between Nen machines. When routing of information and storing of information is payed in grams. also on top of that build a decentralized computing marketplace where anyone can share and rent their unused memories and CPU for grams. and from this many decentralized application can be made. From building a decentralized Metaverse to a decentralized Global General purpose Artificial Intellegent.
Den Brain
When Humanity reach a level of Nen and Zen, where everything is connected, from All humans on earth and their technological artifacts. We can reach what we call the Den Brain. Where the whole planet is seen as a one decentralized consciousness that become increasingly intelligent and efficient overtime in solving the world wide problem like Hunger, Disease, Ressources, and lastly Evil and reaching an ever lasting One Peace. That moment when Humanity flourish in every field and every dimension of Truths out there, and became so resilient that no one, not even Satan himself can corrupt The Den Brain even in thousands of years. And only God whom there is no god except Him who can end it. Humanity will live in Peace until The End of Time
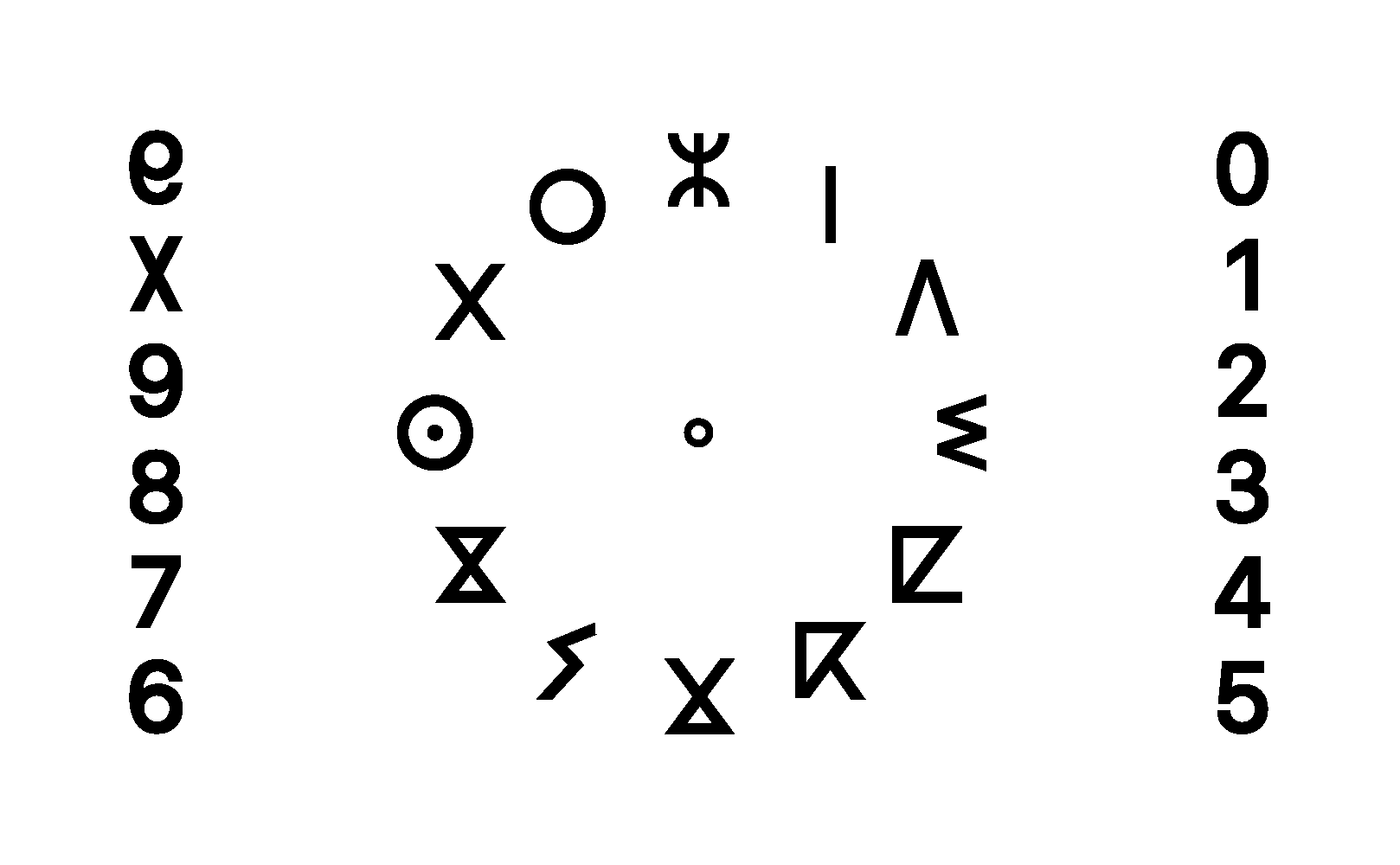
Dozenal base is simply pricing goods and services in base 12 numerical system. Where we use 12 Codes to represent numbers.
Comparing to the Decimal Base system. Dozenal make counting, addition , substraction, multiplication and division of prices very easy with the use of hand phalanges. Which make it the perfect tool for commerce and trading.
Some additional research
Metallic Sold (Between Buyer and Seller)
A metallic Sold is a type sold calculated with the metallic means. It depend on the number of unit someone purchase at the same time.
In exemple of a service that cost 1 unit. We add +61,80% at the price to the base price. We will say that the base price is 1.62 units. Then we propose the sold program as fellow.
| Order | Mettalic | Value | |
| 1 | 1,6180 | 1 | Full Price |
| 2 | 2,4142 | 1,4920 | Buy 1 Get 2nd 50% Free |
| 3 | 3,3027 | 2,0412 | Buy 2 Get 1 Free |
| 4 | 4,2360 | 2,6180 | |
| 5 | 5,1925 | 3,2091 | Buy 3 Get 2 Free |
| 6 | 6,1622 | 3,8084 | |
| 7 | 7,1400 | 4,4127 | |
| 8 | 8,1231 | 5,0203 | Buy 5 Get 3 Free |
| 9 | 9,1097 | 5,6301 | |
| 10 | 10,0990 | 6,2415 | |
| 11 | 11,0901 | 6,8541 | |
| 12 | 12,0827 | 7,4675 | |
| 13 | 13,0764 | 8,0817 | Buy 8 Get 5 Free |
| 14 | 14,0710 | 8,6963 | |
| 15 | 15,0663 | 9,3115 | |
| 16 | 16,0622 | 9,9270 | |
| 17 | 17,0586 | 10,5428 | |
| 18 | 18,0553 | 11,1588 | |
| 19 | 19,0524 | 11,7750 | |
| 20 | 20,0498 | 12,3915 | |
| 21 | 21,0475 | 13,0080 | Buy 13 Get 8 Free |
Exemple of service to use this sold are intellectual Work and repetitive services like repairing of machinery.
It follow the reasonning that the effort of repairing 1 machine compared to 100 machines is not linear but follow a metallic curve. Therefore the price of repairing 1 machine need to be more expensive than (repairing 100 machine)/100.
Competition (Between Spectators and Players)
In a car race of 12 players that compete for a price reward of 1000 unit. The reward should be distributed in a metallic way as fellow.
| Order | Mettalic | Reward Ratio | Reward |
| 1 | 0,6180 | 0,2404 | 240,4019 |
| 2 | 0,4142 | 0,1611 | 161,1201 |
| 3 | 0,3027 | 0,1177 | 117,7732 |
| 4 | 0,2360 | 0,0918 | 91,8253 |
| 5 | 0,1925 | 0,0749 | 74,9104 |
| 6 | 0,1622 | 0,0631 | 63,1225 |
| 7 | 0,1400 | 0,0544 | 54,4783 |
| 8 | 0,1231 | 0,0478 | 47,8854 |
| 9 | 0,1097 | 0,0426 | 42,6990 |
| 10 | 0,0990 | 0,0385 | 38,5164 |
| 11 | 0,0901 | 0,0350 | 35,0741 |
| 12 | 0,0827 | 0,0321 | 32,1928 |
| Total | 2,5708 | Total | 1000 |
For a Duel between two player :
| Order | Mettalic | Reward Ratio | Reward |
| 1 | 0,6180 | 0,5987 | 59,8726 |
| 2 | 0,4142 | 0,4012 | 40,1273 |
| Total | 1,0322 | Total | 100 |
If it is a duel with betting. Where The two player bet 50 which make the Table reward is 100. The first match the winner gain 10 (+20% of his betting) and the loser lose 10 (-20% of his betting). And the loser can ask the winner for revenge. By rebetting what he has left. If he win he will retake what his lost on the previous match. And this Duel can have many match until both players take profit or stop loss. And in the process if a player is caught cheating. He lose all what he is initial bet.
But in the Believe System of Den, the +20% as profit on the betting is an interest charged on the loser. Interest backed by a promise to pay after a loss without any exchange in a good nor service.
To avoid this interest on the Duel, we will define a Duel (and any Competition and Tournament) as an Entertainment Service offer by Players (Sellers) to Spectators (Buyers). It's possible to see it also as an Optimisation Service, where Players compete to find the most optimal solution of a problem. And The Spectators collect the data for research.
The Players are those who offer the service. And the Spectators who pay for the service.
To avoid any Reward Table manipulation and Effort stealing. An individual is forbidden to be a Player and a Spectator at the same time. A Spectator that paid for the service is forbidden to compete. And Players must compete with no fee nor any charges. And all Players must get their reward for the effort they have given and loyalty no matter their rankings.
In the 12 players race car exemple. The 12th player even if he finished last he get 3.2% of the toble reward 32.19. If he finished last in a 360 player race for a 1000 table reward, his reward will be 0.046% of the table reward which is 0.46.
If the Spectators and Players caught a player cheating they have the right to exclude it. Then and only then a player can receive 0 reward.
With this distribution, it's possible to buid applications on top of YKJ-Network to finance Duel, Competition, Tournament, Research, Optimisation etc. And this without the need of a interest based betting.
Exemple of scenario is an application to finance Speed-Running of video games (an Optimisation Service).
If we take Super Mario Bros. from NES. The application must give anyone the right to submit their runs (Videos, File, Data of the Run…) with their wallet addresses.
And the application list the records and the address of the table Super Mario Bros. . If some money is received, it automatically get distributed in a metallic way to the wallet of those who have submited a run according to their rankings.
And then according to the rules that the Spectator set on the application, for exemple a player must play in an original console with the original game, he must give a video of himself playing it etc. A Spectator that have send some money to the table can validate a run. A run can have many validation and many invalidation from Spectators.
In Super Mario Bros, there is in speedrun.com 633 different run submitted. If I submit a run and get 99th place (Mettalic mean of 0,01001). The application will show 0 validation. I need 633^0,01001 = 1 validation from a spectator to receive 100% of the metallic distribution if some one send some money to the game table. (0.02%)
Instead if I beat the world record. I need 633^0,61803 = 54 validations to receive 100% (10.42% of the table) But if I get only 30/54, I will receive 55% of the futur metallic distribution. Because a World Record need to be validated by many Spectators who support the community.
Intellectual Works (Between Authors and Community)
An Intellectual Work is any work than can be copied by humans like : Content, Story, Poetry, Document, File, Code Source, Program, Algorithm, Research, Art, Model, Recipe, Process, Design (of Objects, Clothes, Characters, Interfaces), Music, Image, Video, Movie, Animation, Drawing, Scenario, Game, Strategy, Technique… etc. Or any type of informations that can be copied by people.
In the Believe System of Den, there is no central institution. therefore there is no Copyrights, no Patents and no Trademarks. If a person have made an intellectual effort to reach a particular information. He is the only responsible of the information he made.
For exemple In SpongeBob SquarePants If M. Krabs accidentally leak his recipe of Krabby Patty, his many years of effort in research and development in developing Krabby Patty is vanished.
The most natural way is to sell the recipe as a physical product to people. But If M. Krabs sell the recipe to people individual. Someone will eventually spread it for cheaper price (Because the information can be copied) or even for free to everyone. And M. Krabs will lose most of his effort developing the recipe.
The best solution is to set it in only one transaction between Mr. Krabs and the Gourmet Community which can be any person interested in cooking recipes. Mr. Krabs need to set his price of the recipe of the Krabby Patty. For exemple because he is greddy Mr. Krabs will set his weight in Gold as the price of the recipe (5oz).
And if the Gourmet Community is composed of 10 000 persons. They can arrange to rise 5oz of gold then buy his recipe in one transaction. And after the transaction is set, anyone on earth can read the recipe and use it.
And with applications build on top of YKJ-Network, it's possible to make this transaction trustless and decentralized. Where none of either party can cheat the other.
An other exemple of such application is a mangaka selling chapters of his manga.
First the author, publish 1 to 3 first chapters as introduction to the story to attract people. Then he set price for every new chapter. For exemple the 4th chapter, he worked 72 hours so he set the price of it 6 Rens/Yens. Then people who are interested in his story will support the new community build around the manga and send some money (like I send 0.01 Ren/Yen) to the address of the 4th chapter. And the moment the money received for the chapter is more than 6 Rens/Yens. The 4th chapter get unlocked and anyone on earth can read it.
If the manga get too popular and the community want to make it an anime. They can work together and make an collaboration between scenarist, keyframes, animators, voice actors, sound and visual effect, music, montage to make a decentralized open-to-anyone-to-join animation studio. Where any collaborator of the project set his price for a complete episode. And the community send money to every single collaborator, and they can unlock the episode only if all the collaborators have received the price they have set. And then after the episode is unlocked. Anyone on earth can watch it.
Gungi : A board game with the use of Gold/Silver/Cooper physical coins
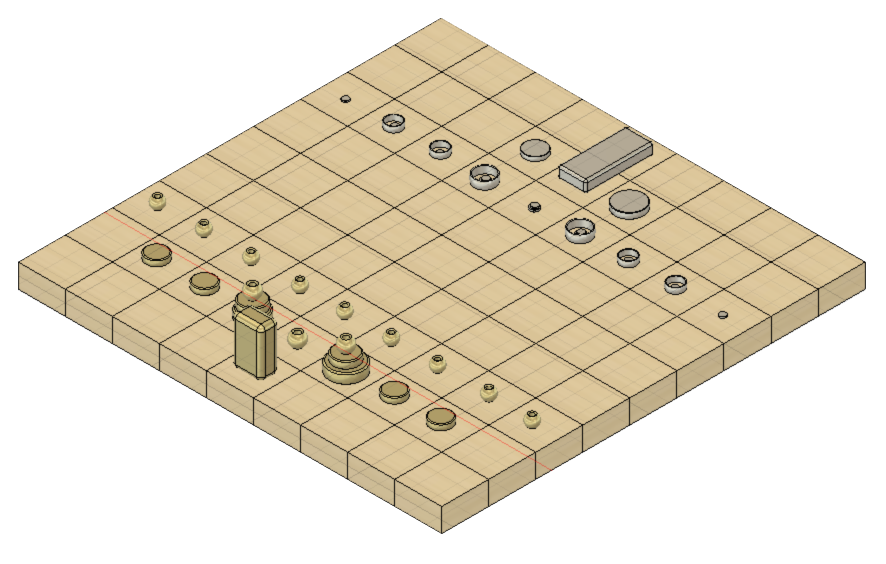
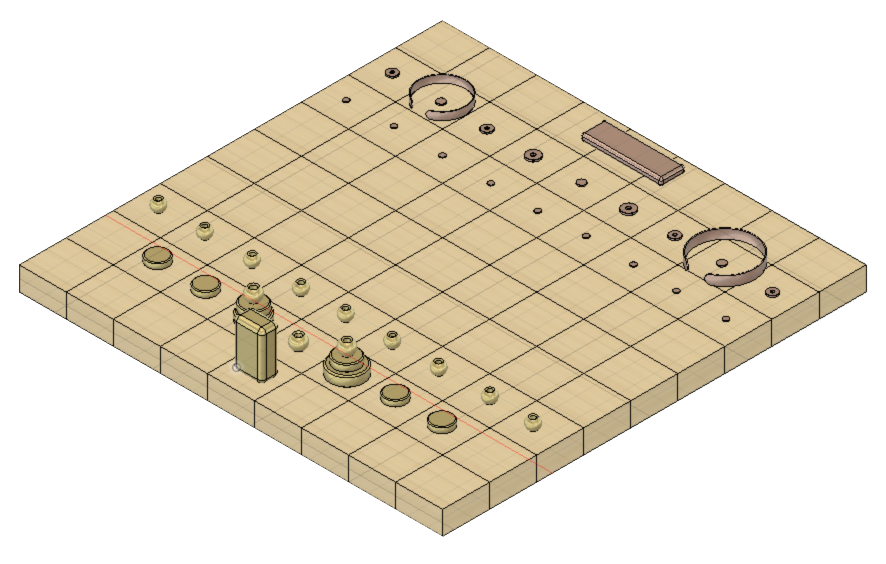
Gungi is a two-player strategy board game on a 9×9 grid that use the physical coins as pieces. A game will be a type of pieces (exemple Gold) againts another type (exemple Silver). The pieces of each type have different move set. And pieces can be put on top of each other to combine move sets.
At the beginning of the game, players choses which type of pieces to uses againts which one, either Gold vs Silver, Silver vs Copper, or Copper vs Gold. They start with an empty board. Each side have 21 pieces in hand : 1 king, 1+1 commanders, 2+4 captains, 3+9 soldiers. They can choose how their pieces will be arranged on their side of the board. Additionally, pieces can be stacked on top of each other, adding a third dimension to the game. Up to two additional pieces can be stacked on top of a piece, for up to 3 pieces in a single column. The objective is to get the "King" (Gungi piece) into checkmate.
(Zen is still under research and development)And this is Zen.
Join us :
Discord - Reddit - Youtube - Twitter
Support us :
Bitcoin : 3Di7NCacvRmsRxxZ8Q6VDoXniVFZBrV8Pw
Ethereum : 0xCBb3ACa68f77437ce8A33bD74E48760018ee1a9a